Implisiittinen derivointi

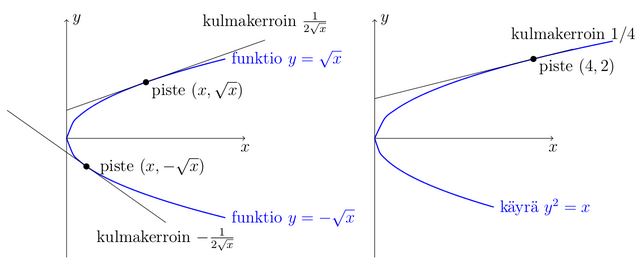
Ratkaisu (eksplisiittisesti). Jos \(y^2 = x\), niin \(y^2 \geq 0\) ja edelleen \(x\geq 0\). Tällöin yhtälöstä \(y^2=x\) voidaan ottaa puolittain neliöjuuri, ja saadaan \(|y|=\sqrt{x}\). Näin ollen käyrä \(y^2=x\) koostuu kahdesta osasta, joita vastaavat funktiot \(y = \sqrt{x}\) ja \(y = -\sqrt{x}\), missä \(x\geq 0\). Kumpikin funktiosta on derivoituva, ja niiden derivaattoina saadaan käyrän kulmakertoimet jokaiselle pisteelle poislukien origo. Erityisesti, tangentin kulmakerroin pisteessä \( (4,2) \) on funktion \(\sqrt{x}\) derivaatta pisteessä \(x=4\). Tangentin kulmakertoimeksi saadaan \(1/4\).

Ratkaisu (implisiittisesti). Käyrä on muotoa \(y(x)^2 = x\), joten jos sen molemmat puolet derivoidaan yhtäsuuruus säilyy, ja saadaan
\[
2 y(x) y'(x) = 1 \quad \textrm{ eli } \quad y'(x) = \frac{1}{2 y(x)}.
\]Huomaa, että \(y(x)^2\) on yhdistetty funktio, jonka derivoimiseksi pitää käyttää ketjusääntöä. Jos käyrällä oleva piste \((x_0,y_0)\) on annettu, niin tätä pistettä vastaava tangentin kulmakerroin saadaan kaavasta \(y'(x_0) = 1/(2y_0)\). Piste \((4,2)\) on käyrällä ja edelleen \( y'(4) = 1/4\).

Ratkaisu (eksplisiittisesti). Jos \(y^2 = x\), niin \(y^2 \geq 0\) ja edelleen \(x\geq 0\). Tällöin yhtälöstä \(y^2=x\) voidaan ottaa puolittain neliöjuuri, ja saadaan \(|y|=\sqrt{x}\). Näin ollen käyrä \(y^2=x\) koostuu kahdesta osasta, joita vastaavat funktiot \(y = \sqrt{x}\) ja \(y = -\sqrt{x}\), missä \(x\geq 0\). Kumpikin funktiosta on derivoituva, ja niiden derivaattoina saadaan käyrän kulmakertoimet jokaiselle pisteelle poislukien origo. Erityisesti, tangentin kulmakerroin pisteessä \( (4,2) \) on funktion \(\sqrt{x}\) derivaatta pisteessä \(x=4\). Tangentin kulmakertoimeksi saadaan \(1/4\).

Ratkaisu (implisiittisesti). Käyrä on muotoa \(y(x)^2 = x\), joten jos sen molemmat puolet derivoidaan yhtäsuuruus säilyy, ja saadaan
\[
2 y(x) y'(x) = 1 \quad \textrm{ eli } \quad y'(x) = \frac{1}{2 y(x)}.
\]Huomaa, että \(y(x)^2\) on yhdistetty funktio, jonka derivoimiseksi pitää käyttää ketjusääntöä. Jos käyrällä oleva piste \((x_0,y_0)\) on annettu, niin tätä pistettä vastaava tangentin kulmakerroin saadaan kaavasta \(y'(x_0) = 1/(2y_0)\). Piste \((4,2)\) on käyrällä ja edelleen \( y'(4) = 1/4\).