Videoita
Videoita syksyltä 2019.
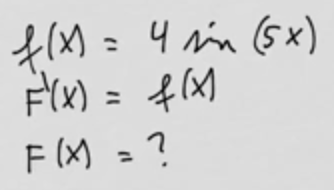youtubeAntiderivaatta 2.Etsitään funktion \(\sin(5x)\) integraalifunktio.
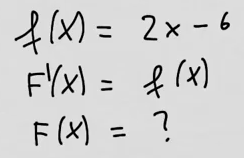youtubeAntiderivaatta 3."Esimerkkifunktiolle löydetään useampia integraalifunktioita. Yleisesti, ""integraalifunktio + vakio"" on myös eräs integraalifunktio."
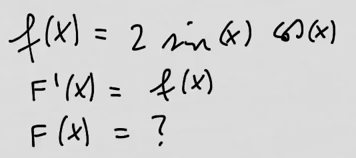youtubeAntiderivaatta 4.Esimerkkifunktiolle löydetään useampia integraalifunktioita, jotka vaikuttavat hyvin erilaisilta. Paljastuu, että nämä eroavat toisistaan pelkästään summattavalla vakiolla.
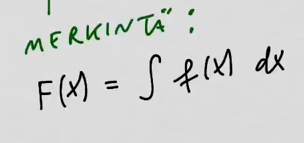youtubeAntiderivaatta 5.Tutustutaan integraalifunktion merkintätapaan. Merkintätapa helpottaa integraalifunktion etsimistä, sillä derivoinnin lineaarisuuden avulla etsiminen voidaan tehdä pala palalta.
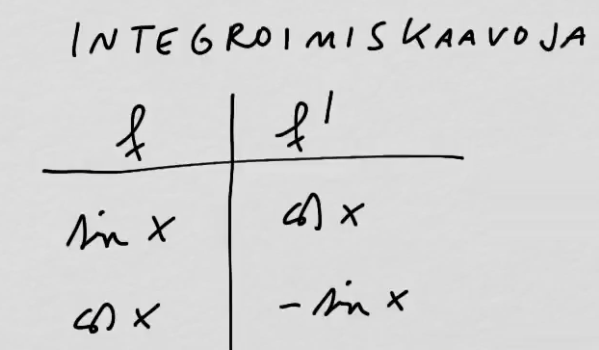youtubeIntegroimiskaavoja.Koska integrointi on derivoinnin käänteisoperaatio, derivoimiskaavoista saadaan helposti paljon integroimiskaavoja.
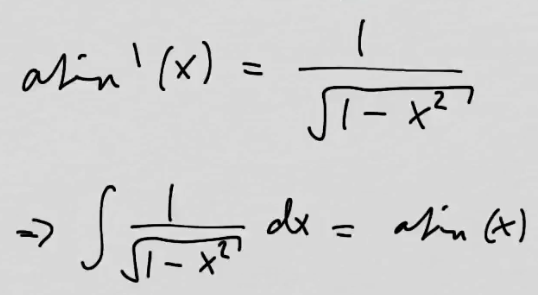youtubeArkussinin ja arkuskosinin derivaatta.Etsitään arkussinin ja arkuskosinin derivaattojen lausekkeet. Tätä varten täytyy käyttää hyväksi trigonometrian kaavoja. Sovelluksena saadaan funktion \(\dfrac{1}{\sqrt{1-x^2}}\) integroimiskaava.
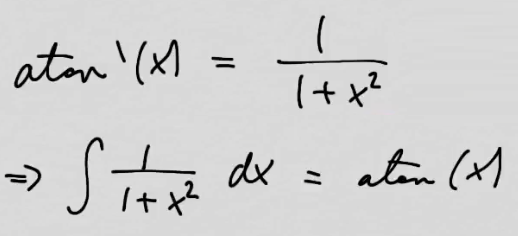youtubeArkustangentin derivaatta.Etsitään arkustangentin derivaatan lauseke. Tätä varten täytyy käyttää hyväksi trigonometrian kaavoja. Sovelluksena saadaan funktion \(\frac{1}{1+x^2}\) integroimiskaava.
youtubeHeittoliikkeen differentiaaliyhtälö.Mallinnetaan heittoliikettä differentiaaliyhtälöllä. Ratkaistaan liikettä kuvaava differentiaaliyhtälö.
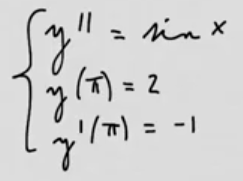youtubeToisen asteen differentiaaliyhtälö.Ratkaistaan eräs toisen asteen differentiaaliyhtälö.
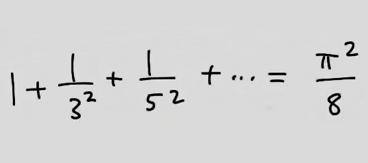youtubeKosinin ääretön tulo.Kosini voidaan esittää sekä sarjakehitelmänä että tulokehitelmänä. Kehitelmien kertoimia vertaamalla voidaan johtaa erään sarjan summa.
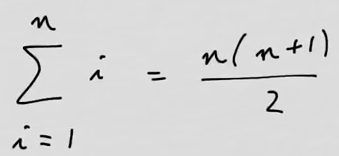youtubeAritmeettisen summan kaava.Todistetaan aritmeettisen summan kaava, joka on yksinkertaisin esimerkki summakaavasta.
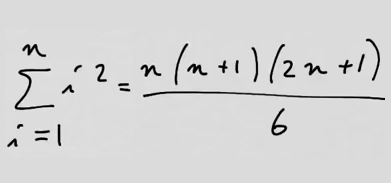youtubeNeliöiden summan kaava.Todistetaan neliöiden summan kaava. Kaavaa tarvitaan esimerkiksi, kun lasketaan käyrän \(y=x^2\) ja \(x\)-akselin välissä oleva pinta-ala Riemannin summilla.
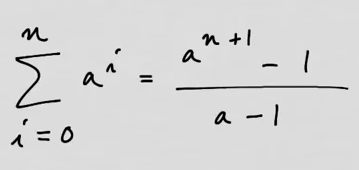youtubeGeometrisen summan kaava.Todistetaan geometrisen summan kaava. Kaavaa tarvitaan esimerkiksi, kun lasketaan käyrän \(y=e^x\) ja \(x\)-akselin välissä oleva pinta-ala Riemannin summilla.
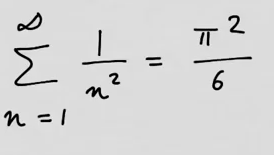youtubeBaselin ongelma.Treenataan indekseihin perustuvia merkintätapoja johtamalla luonnollisten lukujen käänteislukujen summa. Johdossa tarvitaan sinin sarjakehitelmää ja tuloesitystä äärettömänä tulona. Johdetaan summan kaava oivaltavasti, jolloin kuitenkin sivuutetaan paljon yksityiskohtia. (Mitä tarkoittaa äärettömän monen nollasta eroavan luvun summa? Mitä tarkoittaa äärettömän monen ykkösestä eroavan luvun tulo?) Kuuluisa matemaatikko Euler laski summan ensimmäisenä, vuonna 1734.
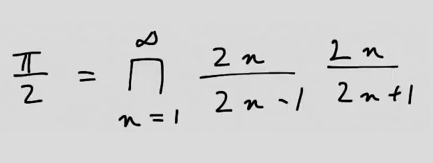youtubeWallisin tulo.Treenataan indekseihin perustuvia merkintätapoja laskemalla ääretön tulo \(\frac{2\cdot 2}{1\cdot 3}\cdot\frac{4\cdot 4}{3\cdot 5}\cdots\) Johdetaan summan kaava oivaltavasti, jolloin kuitenkin sivuutetaan paljon yksityiskohtia. (Mitä tarkoittaa äärettömän monen nollasta eroavan luvun summa? Mitä tarkoittaa äärettömän monen ykkösestä eroavan luvun tulo?) Kaavan todisti Wallis vuonna 1656.
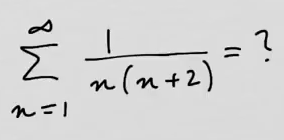youtubeSarja osamurrolla 1.Lasketaan muotoa \(\frac{1}{n(n+2)}\) olevien termien ääretön summa jakamalla termit kahteen osaan, jolloin ongelma yksinkertaistuu. Kyseessä on niinsanottu osamurtokehitelmä, jonka avulla voidaan laskea rationaalifunktioihin liittyviä laskuja, muun muassa integraaleja.
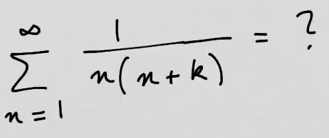youtubeSarja osamurrolla 2.Lasketaan muotoa \(\frac{1}{n(n+k)}\) olevien termien ääretön summa jakamalla termit kahteen osaan, jolloin ongelma yksinkertaistuu. Kyseessä on niinsanottu osamurtokehitelmä, jonka avulla voidaan laskea rationaalifunktioihin liittyviä laskuja, muun muassa integraaleja.
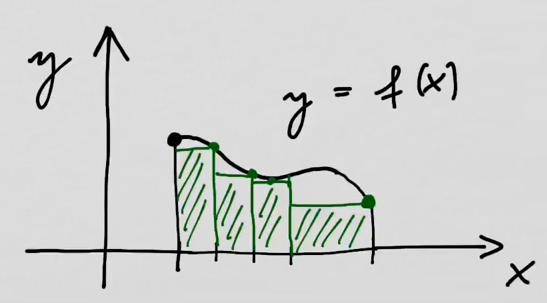youtubeAla- ja yläsumma.Alasumma arvioi funktion kuvaajakäyrän \(y=f(x)\) ja \(x\)-akselin väliin jäävää pinta-alaa kuvaajakäyrän alapuolella olevilla suorakulmioilla. Yläsumma puolestaan kuvaajakäyrän huippujen korkeudelle ulottuvilla suorakulmioilla.
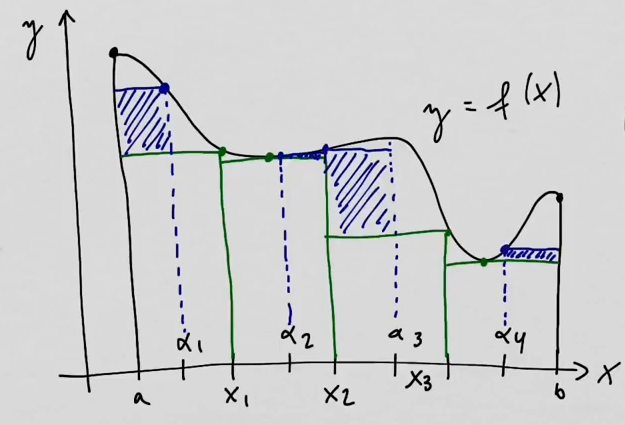
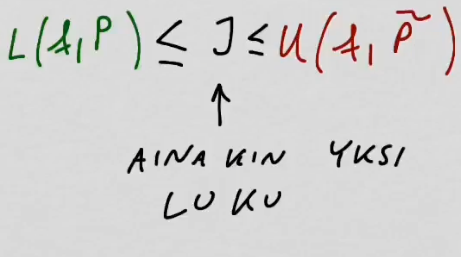youtubeYleinen Riemannin summa.Yleisessä Riemannin summassa suorakulmioiden korkeudet määräytyvät joidenkin evaluaatiopisteiden eli tägien perusteella. Evaluaatiopisteiden ei tarvitse olla esimerkiksi osavälien päätepisteitä tai kuvaajakäyrien huippujen x-koordinaatteja.
youtubeJaon hienontaminen.Jos Riemannin summaan liittyvää jakoa hienontaa/tihentää, niin summa lähestyy kuvaajakäyrän ja \(x\)-akselin väliin jäävän pinta-alan suuruutta.
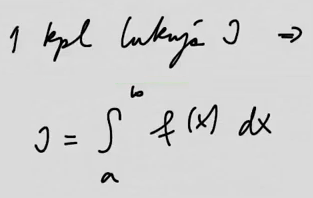youtubeMäärätty integraali.Alasummien lukuarvot ovat korkeintaan mikä tahansa yläsumma. Tätä ominaisuutta käyttäen voidaan määritellä funktion integroituvuus ja edelleen määrätyn integraalin arvo.
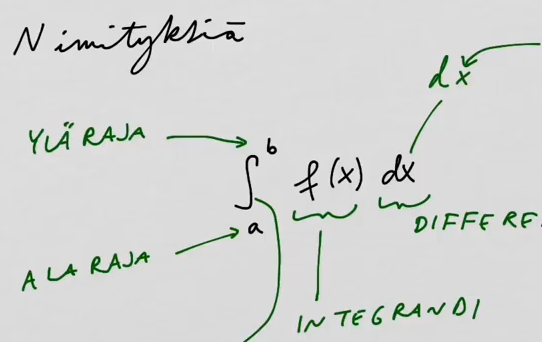youtubeNimityksiä määrättyyn integraaliin liittyen.Määrättyyn integraaliin liittyy monia nimityksiä.
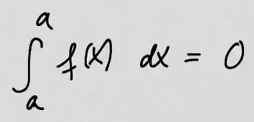youtubeIntegraalin rajat.Integraalin rajoja voidaan manipuloida.
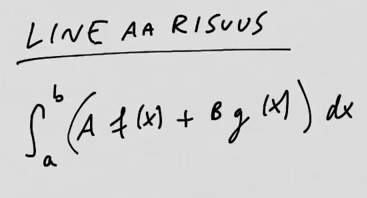youtubeintegraalin lineaarisuus.Summan integraali on integraalien summa. Vakion voi viedä ulos integraalista.
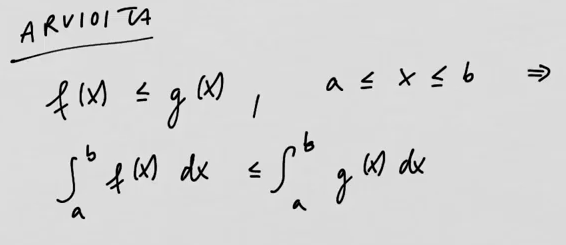youtubeIntegraalien arvioita.Suuremman funktion integraali on suurempi. Jos integrandista otetaan itseisarvo, saadaan vähintään yhtä suuri integraalin arvo.
youtubeJensenin epäyhtälö.Konveksien funktioiden avulla saadaan arvioita integraaleille.
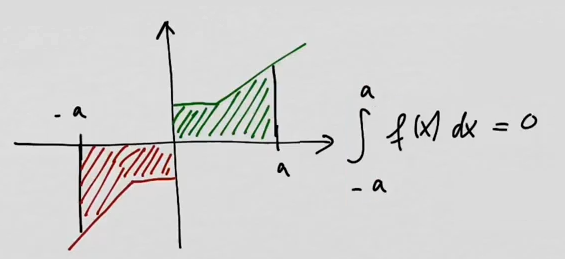
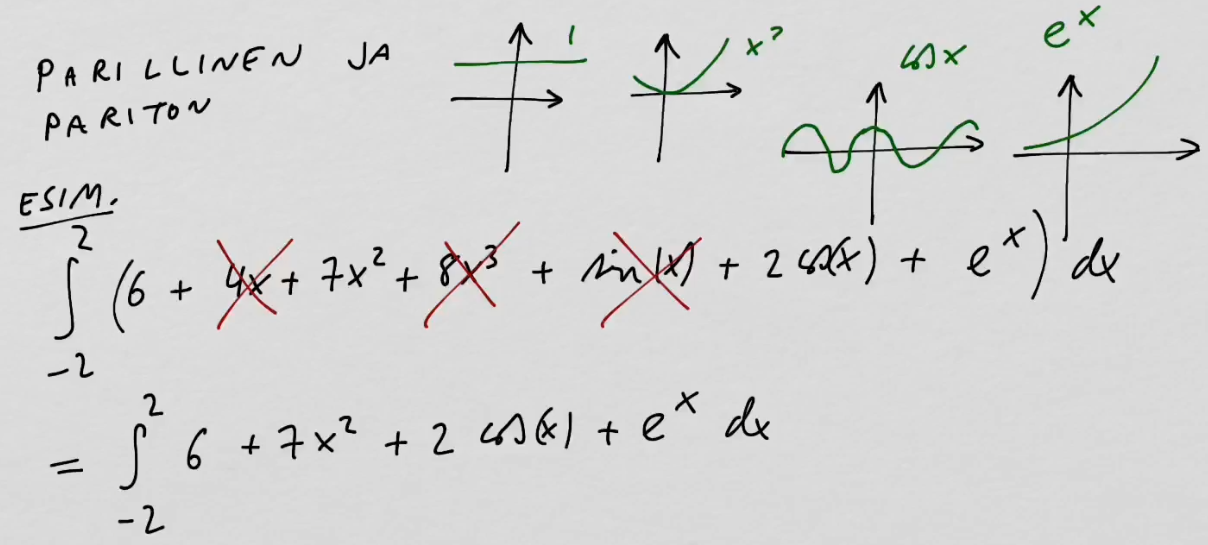youtubeparillinen ja pariton.Jos integroidaan välin \([-a,a]\) yli, niin parittoman funktion integraalista tulee nolla ja parillisen funktion integraali on kaksi kertaa integraali välin \([0,a]\) yli.
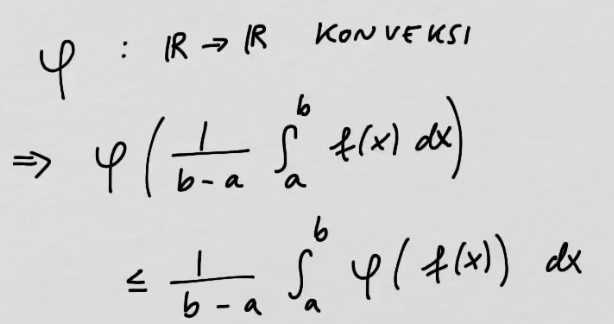youtubeparillinen sovellus.Jos integroidaan välin [-a,a] yli, niin integraalia voi sieventää parittomien ja parillisten funktioiden tapauksessa.
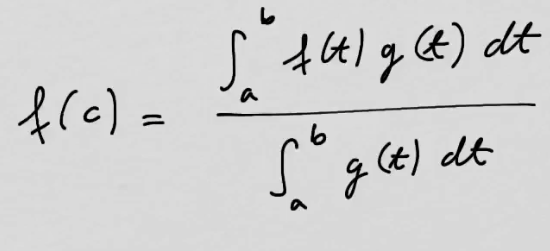youtubeIntegraalilaskennan väliarvolause kahden funktion tulolle.Integraalilaskennan väliarvolauseen yleistys tilanteeseen, jossa integrandina on kahden funktion tulo. Tuloksena saadaan toisen funktion painotettu keskiarvo integroimisvälillä.
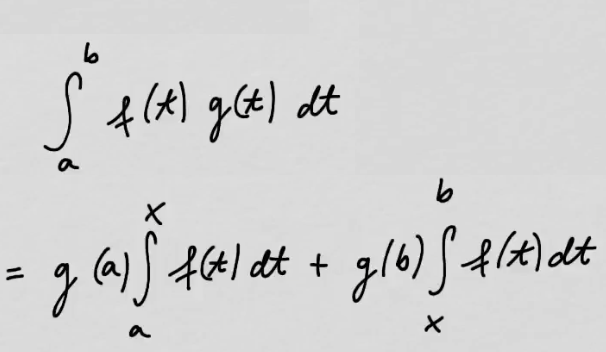youtubeIntegraalilaskennan toinen väliarvolause.Eräs esimerkki integraalilaskennan väliarvolauseen toisenlaisesta versiosta.
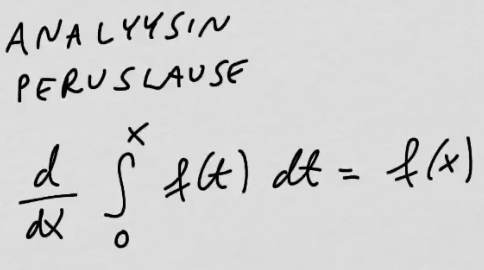youtubeAnalyysin peruslause, esimerkkejä.Esimerkkejä analyysin peruslauseen käyttämisestä.
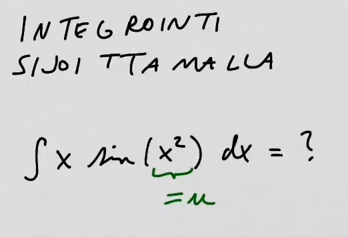youtubeIntegrointi sijoittamalla 1.Integroidaan sijoittamalla \(x\sin(x^2)\).
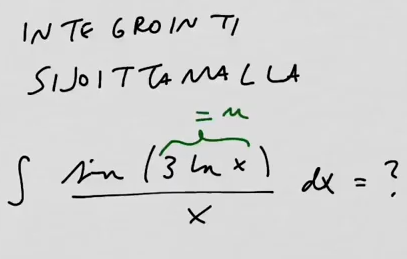
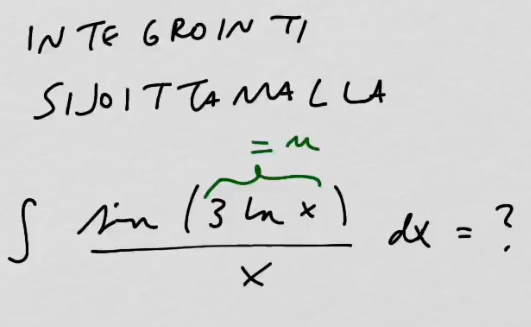
youtubeIntegrointi sijoittamalla 2.Integroidaan sijoittamalla \(\sin(3\ln(x))/x\).
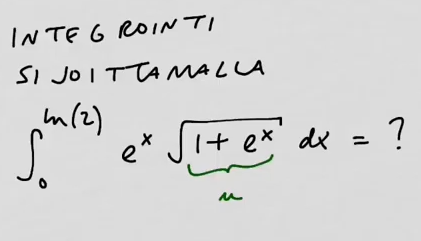youtubeIntegrointi sijoittamalla 3.Integroidaan määrätty integraali sijoittamalla. Muutetaan integroimisrajat.
youtubeIntegrointi sijoittamalla 4.Integroidaan määrätty integraali sijoittamalla. Tehdään takaisinsijoitus ja sen jälkeen sijoitetaan alkuperäiset integroimisrajat.
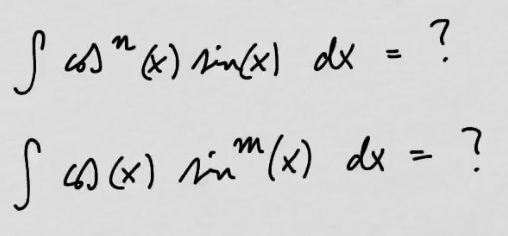youtubeSinin ja kosinin tulon integroiminen 1.Integroidaan \(\cos(x)^n\sin(x)\) ja \(\cos(x)\sin(x)^m\).
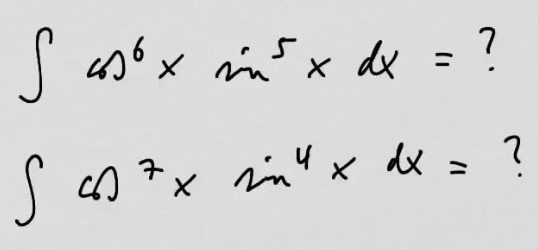youtubeSinin ja kosinin tulon integroiminen 2.Integroidaan \(\cos(x)^n\sin(x)^m\), kun \(n\) tai \(m\) on pariton.
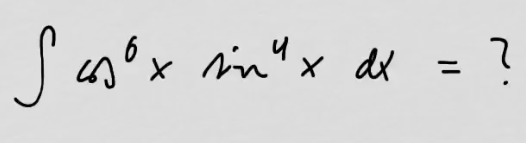youtubeSinin ja kosinin tulon integroiminen 3.Yritetään integroida \(\cos(x)^n\sin(x)^m\), kun \(n\) ja \(m\) ovat parillisia.
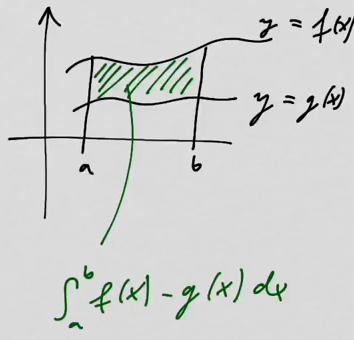youtubeTasoalueen pinta-ala.Funktioiden kuvaajien rajoittaman tasoalueen pinta-ala voidaan laskea integroimalla.
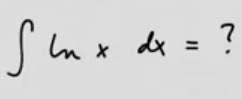youtubeOsittaisintegroidaan funktio ln(x).Luonnollisen logaritmin integraalifunktio saadaan laskettua muun muassa osittaisintegroimalla.
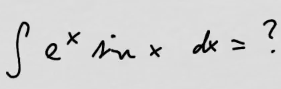youtubeOsittaisintegroidaan exp(x)sin(x).Lasketaan funktion \(exp(x)sin(x)\) integraali. Tällöin joudutaan osittaisintegroimaan kahdesti.
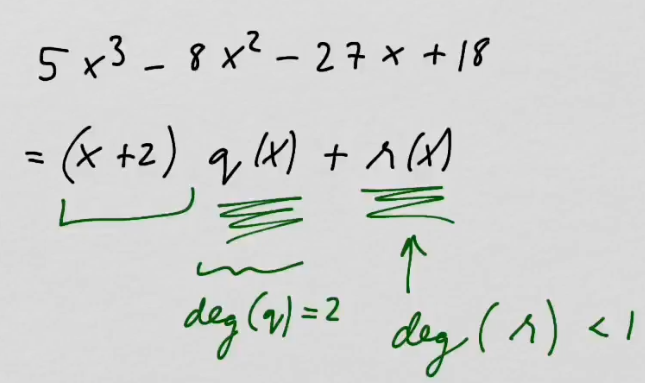youtubeJakoyhtälö polynomeille.Jos korkeampaa astetta oleva polynomi jaetaan matala-asteisemmalla, millainen polynomi on osamäärä ja millainen polynomi on jakojäännös?
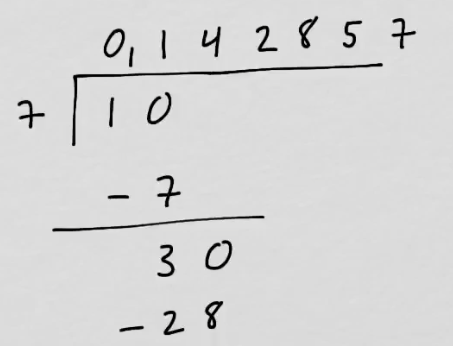youtubeJakokulmassa jakaminen."Palautetaan mieleen kuinka lukuja jaetaan jakokulmassa. Huomataan, että lukujen \(\frac{1}{7},\quad \frac{2}{7},\ldots\) desimaalikehitelmät koostuvat pätkistä ""142857""."
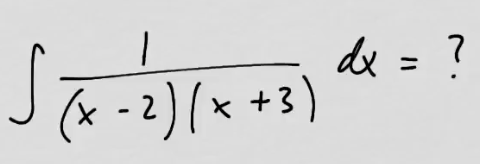youtubeRationaalifunktion integroiminen 1.Integroidaan \(\frac{1}{p(x)}\), jossa \(p(x)=(x-a)(x-b)\).
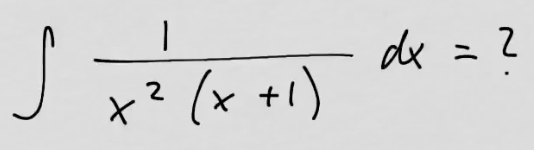youtubeRationaalifunktion integroiminen 2.Integroidaan \(\frac{1}{p(x)}\), jossa \(p(x)=(x-a)^2(x-b)\).
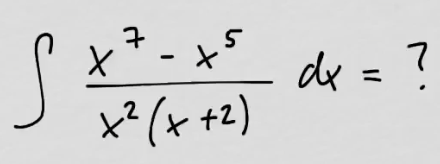youtubeRationaalifunktion integroiminen 3.Integroidaan monimutkainen rationaalifunktio.
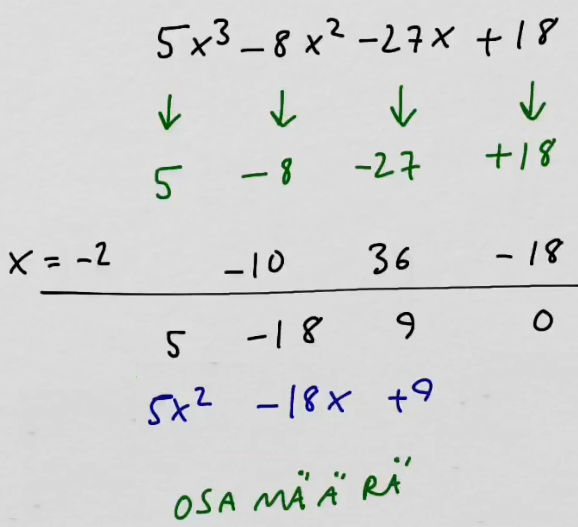youtubeHornerin kaavio 1.Jaetaan polynomi monomilla. Vaihtoehtoinen tapa polynomien jakokulmalle.
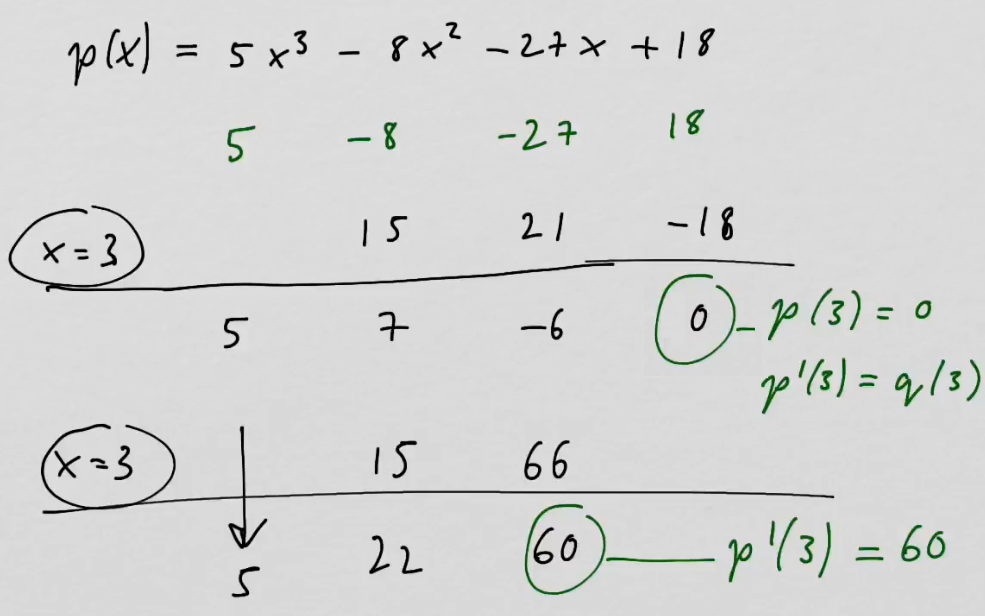youtubeHornerin kaavio 2.Hornerin kaaviolla voidaan tehokkaasti laskea polynomin ja polynomin derivaatan arvo annetussa pisteessä.
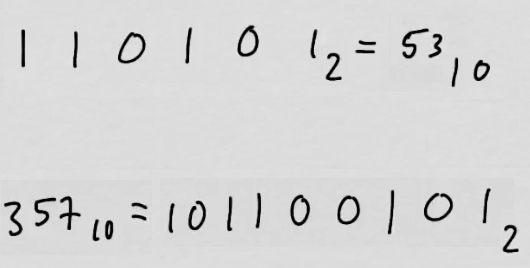youtubeKantaluvun vaihtaminen.Luku voidaan esittää eri kantalukujen avulla. Jos \(a
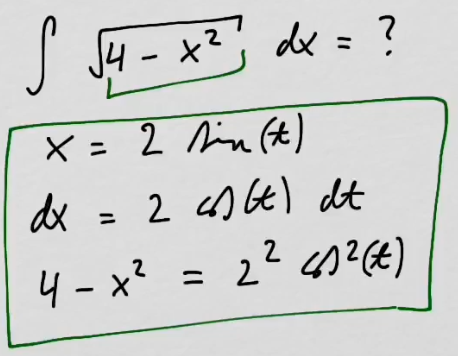youtubeIntegrointi trigonometrisella sijoituksella.Lasketaan esimerkkejä trigonometrisilla sijoituksilla.
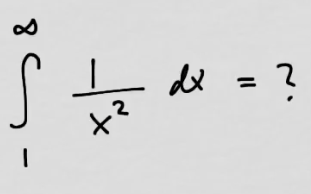youtubeEpäoleellinen integraali rajoittamattoman välin yli.Lasketaan epäoleellisia integraaleja.
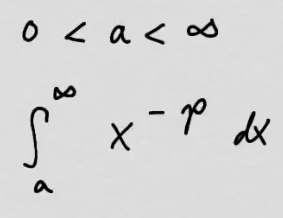youtubep-integraali rajoittamattoman välin yli.Integroidaan funktiota \(\frac{1}{x^p}\) välin \([a,\infty]\) yli.
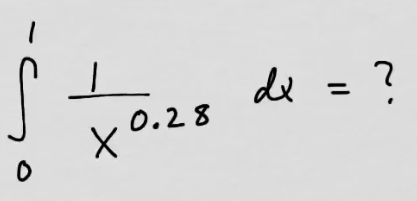youtubeEpäoleellinen integraali rajoittamattomasta funktiosta.Lasketaan epäoleellisia integraaleja.
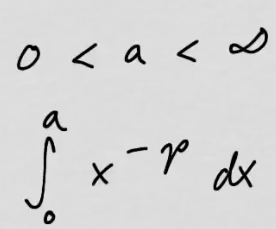youtubep-integraali origon ympäristössä.Integroidaan funktiota \(\frac{1}{x^p}\) välin \([0,a]\) yli.
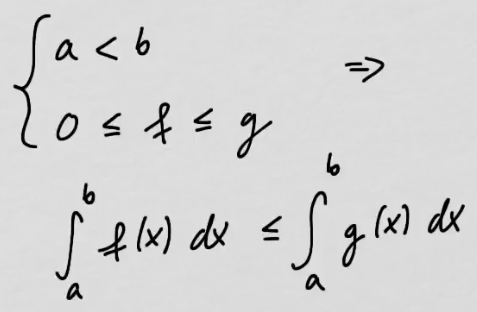youtubeIntegraalien vertailuperiaate.Jos integrandi on monimutkainen, sitä voidaan arvioida yksinkertaisemmaksi. Jos yksinkertaisemman funktion integraali on äärellinen tai ääretön, niin saadaan tietoa alkuperäisen integraalin äärellisyydestä.
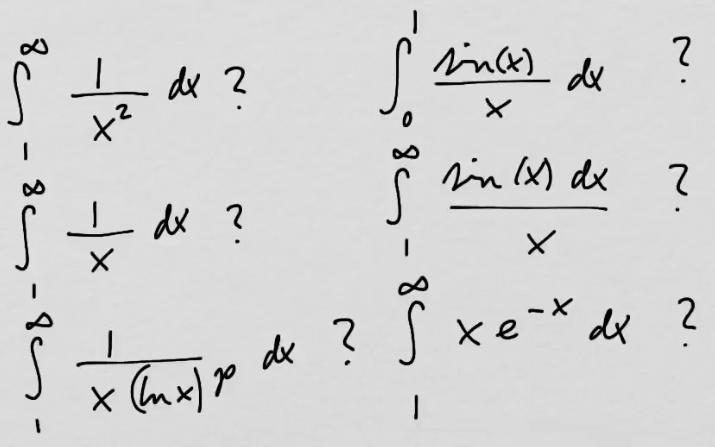youtubeOnko integraali äärellinen?.Tarkastellaan esimerkkejä integraaleista, joiden arvo on äärellinen tai ääretön.
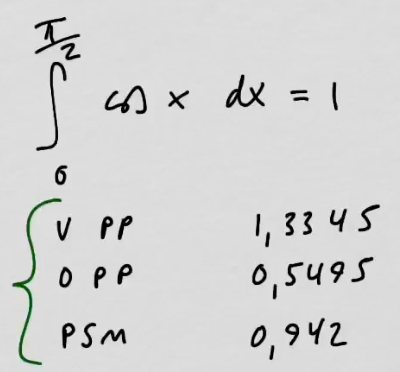youtubePäätepistemenetelmät ja puolisuunnikasmenetelmä.Käydään läpi vasen ja oikea päätepistemenetelmä sekä näiden keskiarvo, puolisuunnikasmenetelmä.
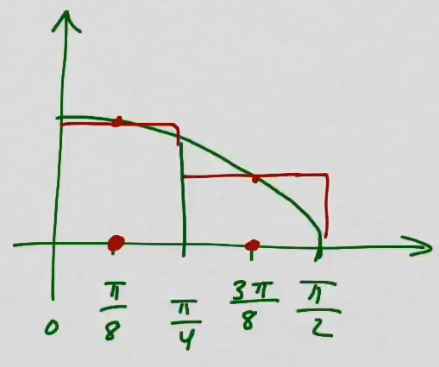youtubeKeskipistemenetelmä.Tarkastellaan keskipistemenetelmää.
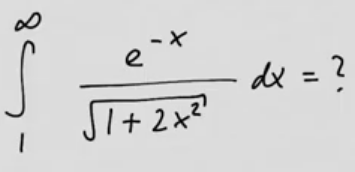youtubeEpäoleellinen integraali numeerisesti.Lasketaan epäoleellinen integraali numeerisesti. Integraali jaetaan integraaliksi äärellisen välin yli sekä häntäintegraaliksi. Integraali äärellisen välin yli osataan laskea numeerisesti. Häntäintegraalia tulisi osata arvioida.
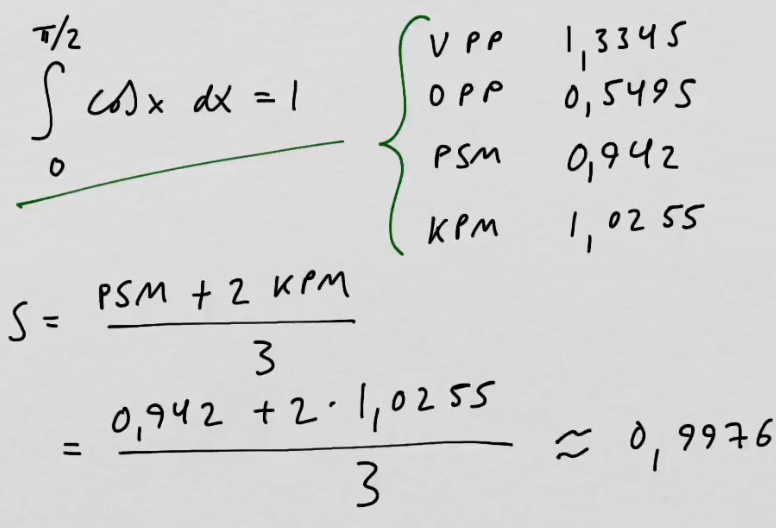youtubeSimpsonin menetelmä 1.Simpsonin säännön johtaminen muista numeerisista integrointimenetelmistä.
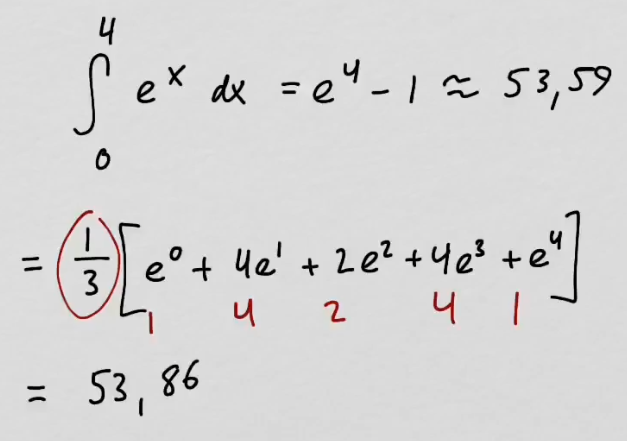youtubeSimpsonin menetelmä 2.Simpsonin säännön soveltaminen eksponenttifunktion integraaliin.
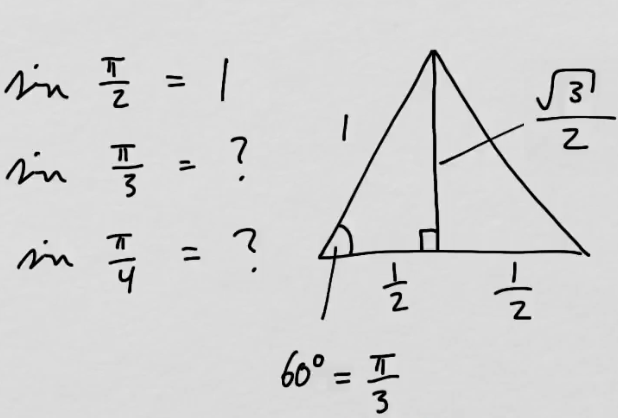youtubeSinin arvoja.Lasketaan arvoja \(sin\bigg(\frac{\pi}{n}\bigg)\) muistikolmioiden avulla.
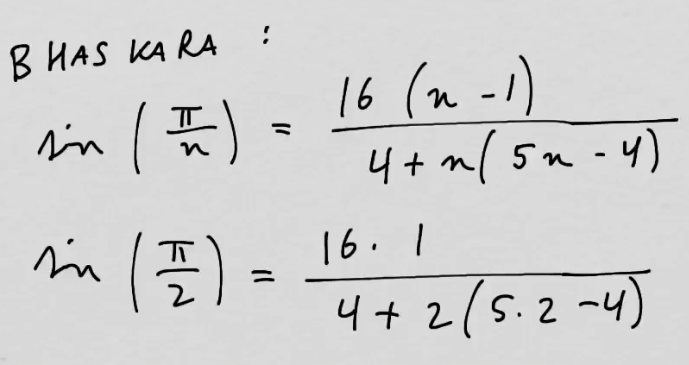youtubeBhaskaran approksimaatio.Lasketaan arvoja \(sin\bigg(\frac{\pi}{n}\bigg)\) Bhaskaran approksimaation avulla.
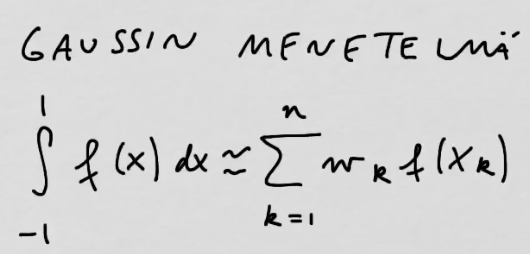youtubeGaussin kvadratuuri.Integraaleja voidaan laskea numeerisesti Gaussin kvadratuurilla.
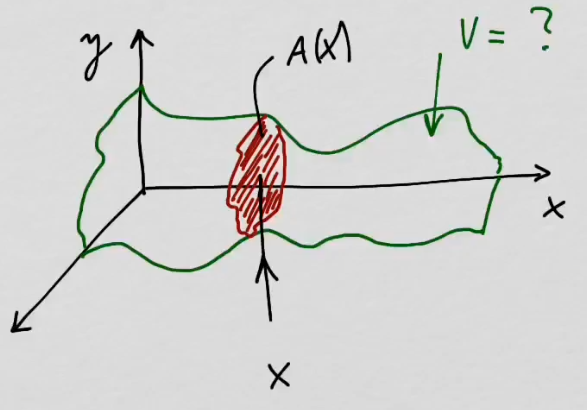youtubeTilavuus siivuttamalla.Jos tunnetaan kappaleen poikkileikkauksen pinta-ala joka kohdassa, voidaan kappaleen tilavuus laskea integroimalla.
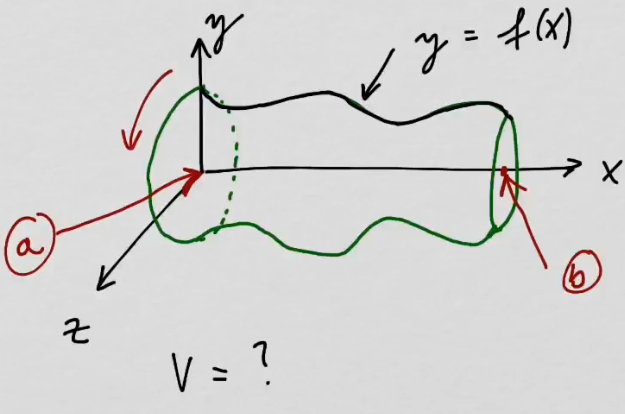youtubePyörähdyskappaleen tilavuus.Pyörähdyskappaleen tilavuus voidaan laskea integroimalla.
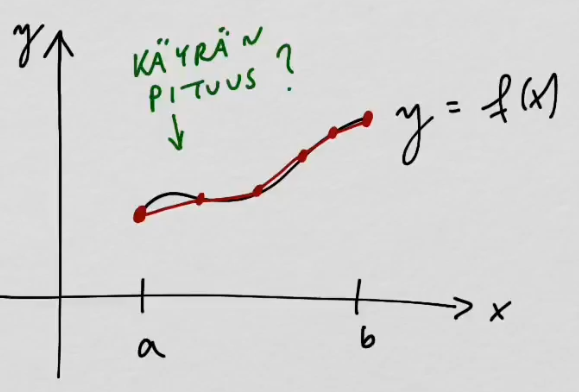youtubeKäyrän pituus integroimalla.Käyrän pituus voidaan laskea integroimalla.
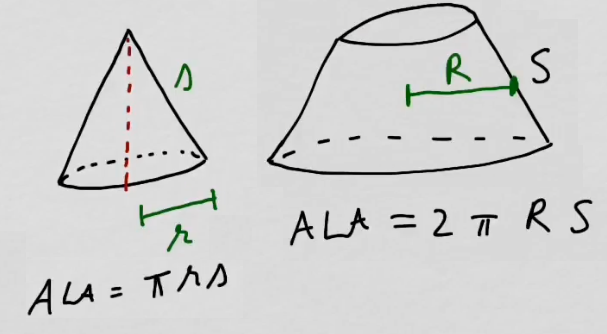youtubeKartion pinnan ala.Tarkastellaan kartion ja katkaistun kartion pinta-aloja. Tämä liittyy läheisesti pyörähdyskappaleen pinta-alan laskemiseen.
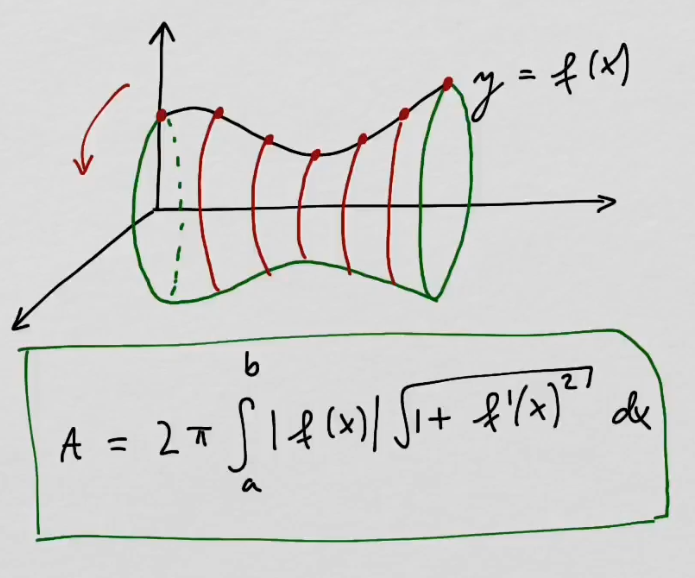youtubePyörähdyskappaleen pinta-ala.Lasketaan pyörähdyskappaleen pinta-ala integroimalla.
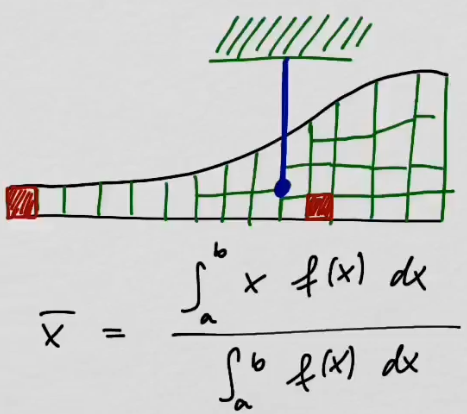youtubeMassakeskipisteen x-koordinaatti.Perustellaan massakeskipisteen \(x\)-koordinaatin kaava.
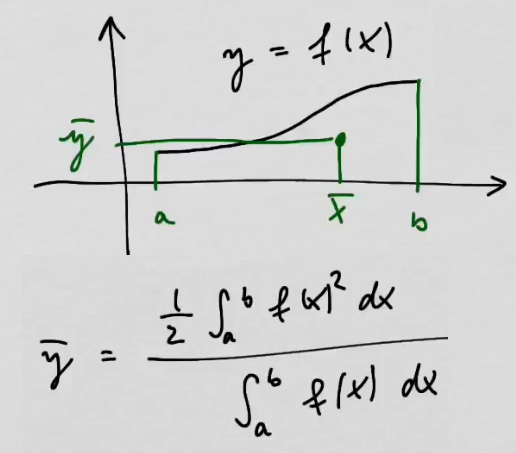youtubeMassakeskipisteen y-koordinaatti.Perustellaan massakeskipisteen \(y\)-koordinaatin kaava.
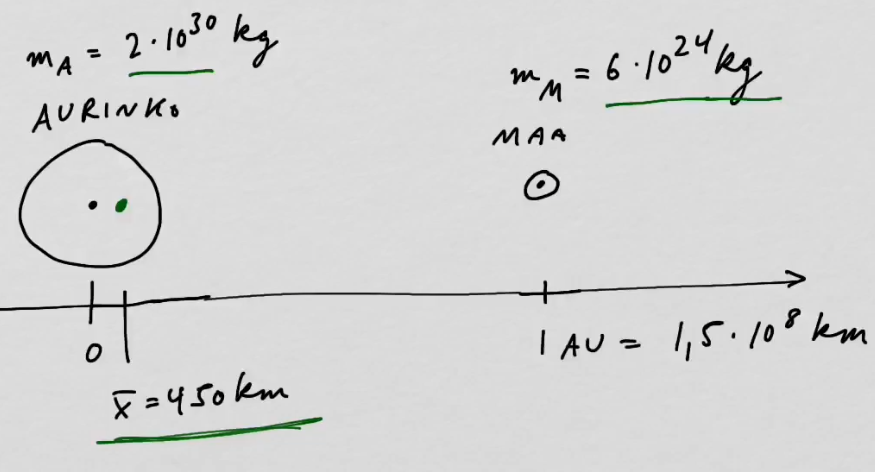youtubeMassakeskipiste Aurinko-Maa-systeemille.Koko systeemin massakeskipiste saadaan osien massakeskipisteiden painotettuna keskiarvona.
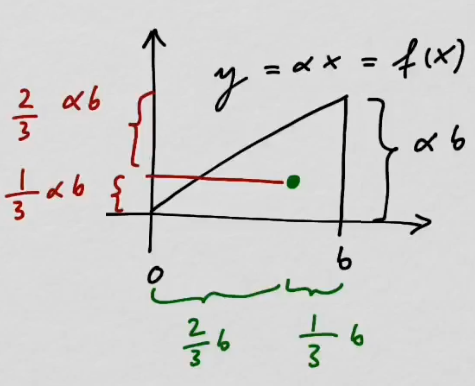youtubeKolmion massakeskipiste.Kolmion massakeskipiste sijaitsee mediaanien leikkauspisteessä.
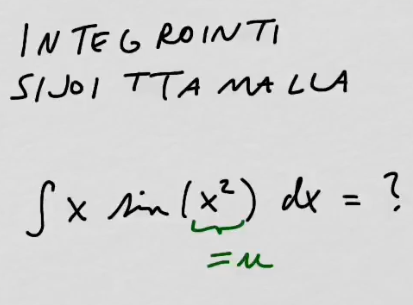youtubePappuksen tilavuuslause.Pyörähdyskappaleen tilavuus voidaan laskea kertomalla massakeskipisteen kulkema matka alueen pinta-alalla.
youtubePappuksen tilavuuslauseen todistus.Todistetaan Pappuksen tilavuuslause.
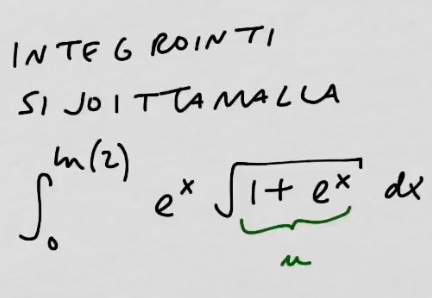youtubePappuksen pinta-alalause.Pyörähdyskappaleen tilavuus voidaan laskea kertomalla käyrän massakeskipisteen kulkema käyrän pituudella.
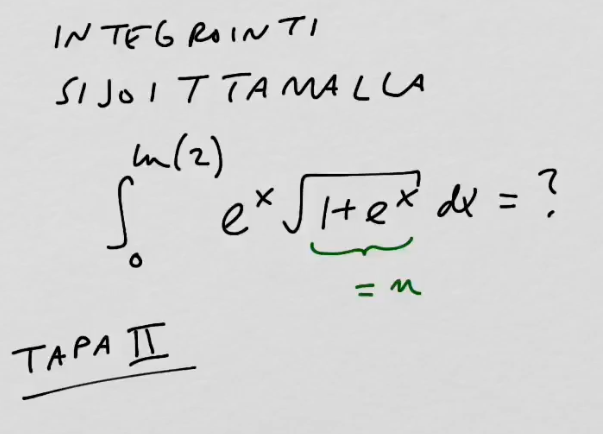youtubePappuksen pinta-alalauseen todistus.Todistetaan Pappuksen pinta-alalause.
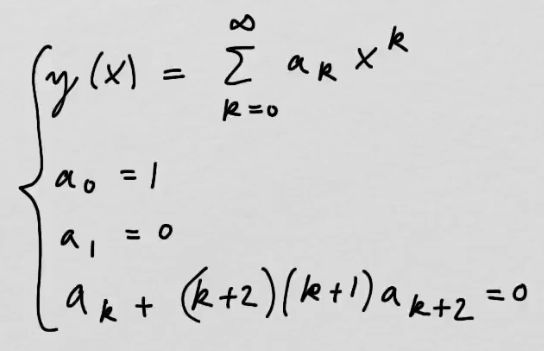youtubeFrobeniuksen sarjamenetelmä.Differentiaaliyhtälöitä voidaan ratkaista tekemällä yrite, joka on potenssisarja.
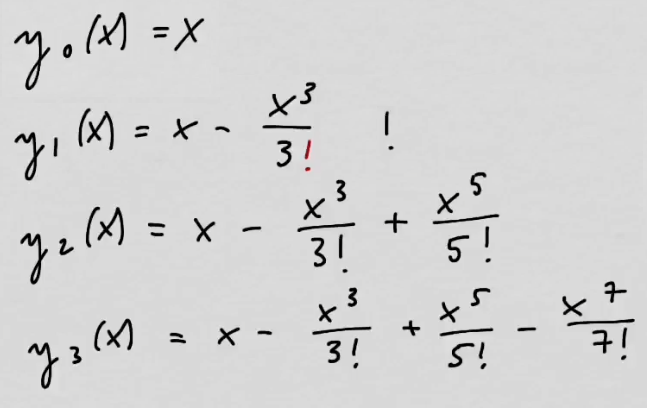youtubePicardin interaatiomenetelmä.Differentiaaliyhtälöitä voidaan iteroiduilla integraaleilla.
